Chapter 21 Stochastic Biological Systems
21.1 Introducing stochastic effects
Up to this point we have studied deterministic differential equations. We use the word deterministic because given an initial condition and parameters, the solution trajectory is known. In this part we are going to study stochastic differential equations or SDEs for short. A stochastic differential equation means that the differential equation is subject to random effects - either in the parameters (which may cause a change in the stability for a time) or in the variables themselves.
Stochastic differential equations can be studied using computational approaches. This part will give you an introduction to SDEs with some focus on solution techniques, which I hope you will be able to apply in other contexts relevant to you. Understanding how to model SDEs requires learning some new mathematics and approaches to numerical simulation. Let’s get started!
21.2 A discrete dynamical system
Let’s focus on an example that involves discrete dynamical systems. Moose are large animals (part of the deer family), weighing 1000 pounds, that can be found in Northern Minnesota. The moose population was 8000 in the early 2000s, but recent surveys show the population is maybe stabilized at 3000.
A starting model that describes their population dynamics is the discrete dynamical system in Equation (21.1):
\[\begin{equation} M_{t+1} = M_{t} + b \cdot M_{t} - d \cdot M_{t}, \tag{21.1} \end{equation}\]
where \(M_{t}\) is the population of the moose in year \(t\), and \(b\) the birth rate and \(d\) the death rate. Equation (21.1) can be reduced down to \(M_{t+1}=r M_{t}\) where \(r=1+b-d\) is the net birth/death rate. This model states that the population of moose in the next year is proportional to the current population.
Equation (21.1) is a little bit different from a continuous dynamical system, but can be simulated pretty easily by defining a function.
M0 <- 3000 # Initial population of moose
N <- 5 # Number of years we simulate
moose <- function(r) {
out_moose <- array(M0, dim = N+1)
for (i in 1:N) {
out_moose[i + 1] <- r * out_moose[i]
}
return(out_moose)
}Notice how the function moose returns the current population of moose after \(N\) years with the net birth rate \(r\). Let’s take a look at the results for different values of \(r\) (Figure 21.1).
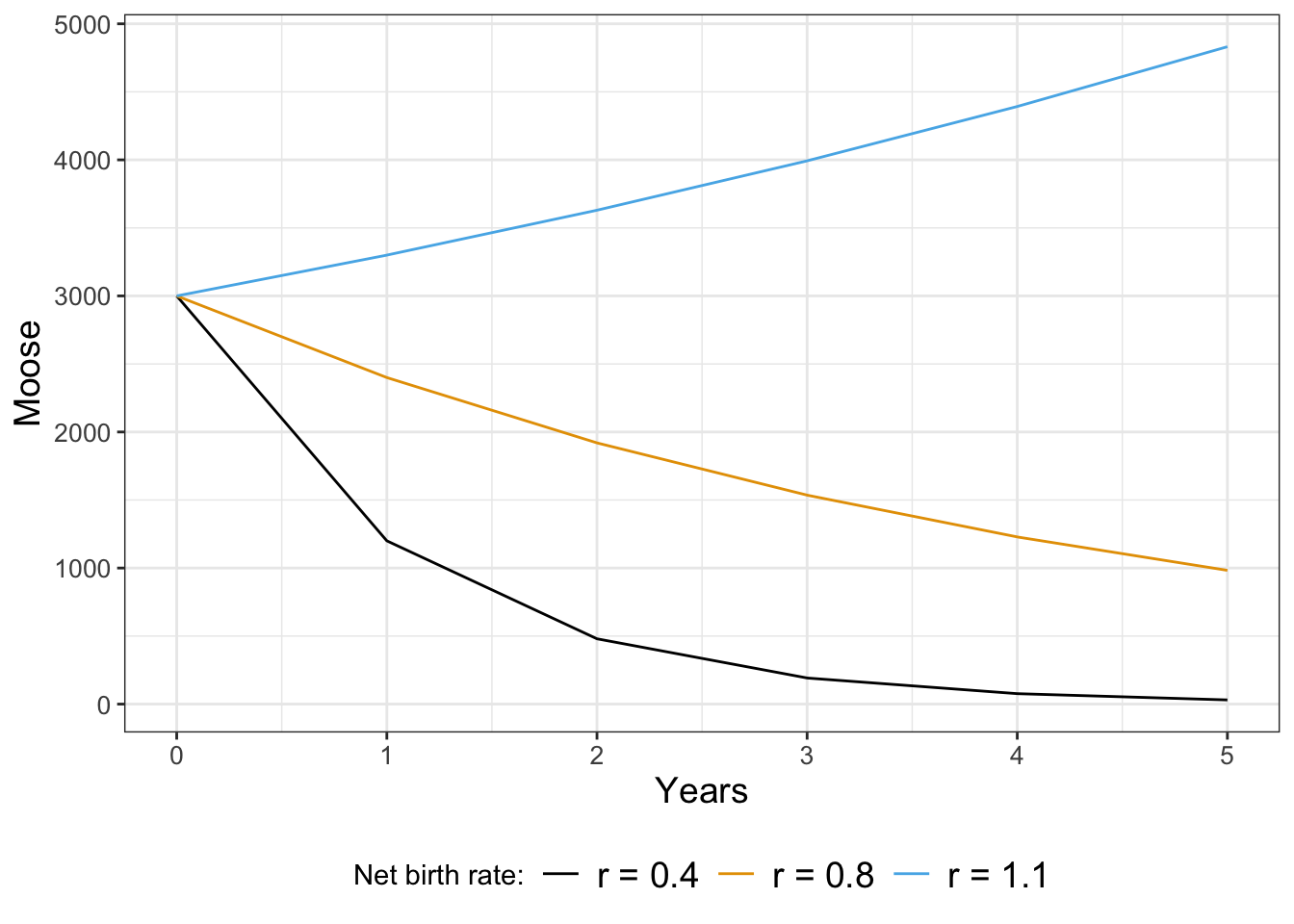
FIGURE 21.1: Simulation of the moose population with different birth rates.
Notice how for some values of \(r\) the population starts to decline, stay the same, or increase. To analyze Equation (21.1), just like with a continuous differential equation we want to look for solutions that are in steady state, or ones where the population is staying the same. In other words this means that \(M_{t+1}=M_{t}\), or \(M_{t}=rM_{t}\). If we simplify this expression this means that \(M_{t}-r M_{t}=0\), or \((1-r)M_{t}=0\). Assuming that \(M_{t}\) is not equal to zero, then this equation is consistent only when \(r=1\). This makes sense: we know \(r=1-b-d\), so the only way this can be one is if \(b=d\), or the births balance out the deaths.
Okay, so we found our equilibrium solution. The next goal is to determine the general solution to Equation (21.1). In Chapter 7 for continuous differential equations, a starting point for a general solution was an exponential function. For discrete dynamical systems we will also assume a general solution is exponential, but this time we represent the solution as \(M_{t}=M_{0} \cdot v^{t}\), which is an exponential equation. The parameter \(M_{0}\) is the initial population of moose (here it equals 3000). Now let’s determine \(v\) in Equation (21.1):
\[\begin{equation} M_{t+1} = r M_{t} \rightarrow 3000 \cdot v^{t+1} = r \cdot 3000 \cdot v^{t} \end{equation}\]
Our goal is to figure out a value for \(v\) that is consistent with this expression. Just like we did with continuous differential equations we can arrange the following equation, using the fact that \(v^{t+1}=v^{t}\cdot v\):
\[\begin{equation} 3000 v^{t} (v-r) = 0 \end{equation}\]
Since we assume \(v\neq 0\), the only possibility is if \(v=r\). Equation (21.2) represents the general solution for Equation (21.1):
\[\begin{equation} M_{t}=3000 r^{t} \tag{21.2} \end{equation}\]
We know that if \(r>1\) we have exponential growth exponential decay when \(r<1\) exponential decay, consistent with our results above.
There is some comfort here: just like in continuous systems we find eigenvalues that determine the stability of the equilibrium solution. For discrete dynamical systems the stability is based on the value of an eigenvalue relative to 1 (not 0). Note: this is a good reminder to be aware if the model is based in continuous or discrete time!
21.3 Environmental stochasticity
It may be the case that environmental effects drastically change the net birth rate from one year to the next. For example during snowy winters the net birth rate changes because it is difficult to find food (Carroll 2013). For our purposes, let’s say that in snowy winters \(r\) changes from \(1.1\) to \(0.7\). This would be a pretty drastic effect on the system - when \(r=1.1\) the moose population grows exponentially and when \(r=0.7\) the moose population decays exponentially.
A snowy winter occurs randomly. One way to model this randomness is to create a conditional statement based on the probability of it being snowy, defined on a scale from 0 to 1. How we implement this is by writing a function that draws a uniform random number each year and adjust the net birth rate:
# We use the snowfall_rate as an input variable
moose_snow <- function(snowfall_prob) {
out_moose <- array(M0, dim = N+1)
for (i in 1:N) {
r <- 1.1 # Normal net birth rate
if (runif(1) < snowfall_prob) { # We are in a snowy winter
r <- 0.7 # Decreased birth rate
}
out_moose[i + 1] <- r * out_moose[i]
}
return(out_moose)
}Figure 21.2 displays different solution trajectories of the moose population over time for different probabilities of a deep snowpack.
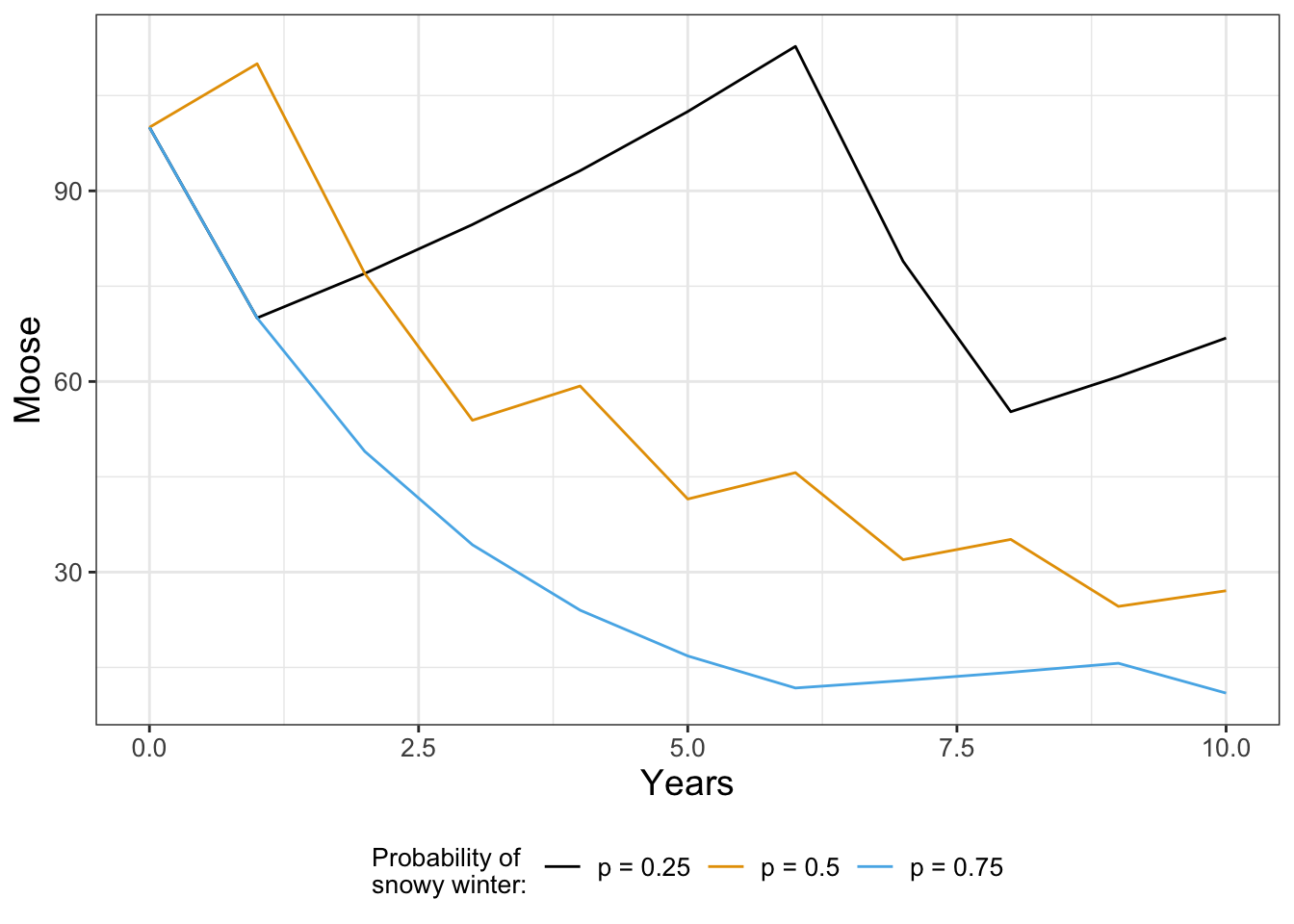
FIGURE 21.2: Moose populations with different probability of adjusting to deep snowpacks.
If you tried generating Figure 21.2 on your own you would not obtain the same figure. We are drawing random numbers for each year, so you should have different trajectories. While this may seem like a problem, one key thing that we will learn later in Chapter 22 is there is a stronger underlying signal when we compute multiple simulations and then compute an ensemble average.
As you can see when the probability of a snowy winter is very high (\(p = 0.75\)), the population decays exponentially. If that probability is lower, the moose population can still increase, but one bad year does knock the population down.
21.4 Discrete systems of equations
Another way to extend Equation (21.1) is to account for both adult (\(M\)) and juvenile (\(J\)) moose populations with Equation (21.3):
\[\begin{equation} \begin{split} J_{t+1} &=f \cdot M_{t} \\ M_{t+1} &= g \cdot J_{t} + p \cdot M_{t} \end{split} \tag{21.3} \end{equation}\]
Equation (21.3) is a little different from (21.1) because it includes juvenile and adult moose populations, which have the following parameters:
- \(f\): represents the birth rate of new juvenile moose
- \(g\): represents the maturation rate of juvenile moose
- \(p\): represents the survival probability of adult moose
We can code up this model using R in the following way:
M0 <- 900 # Initial population of adult moose
J0 <- 100 # Initial population of juvenile moose
N <- 10 # Number of years we run the simulation
moose_two_stage <- function(f, g, p) {
# f: birth rate of new juvenile moose
# g: maturation rate of juvenile moose
# p: survival probability of adult moose
# Create a data frame of moose to return
out_moose <- tibble(
years = 0:N,
adult = M0,
juvenile = J0
)
# And now the dynamics
for (i in 1:N) {
out_moose$juvenile[i + 1] <- f * out_moose$adult[i]
out_moose$adult[i + 1] <-
g * out_moose$juvenile[i] + p * out_moose$adult[i]
}
return(out_moose)
}To simulate the dynamics we just call the function moose_two_stage and plot in Figure 21.3:
moose_two_stage_rates <- moose_two_stage(
f = 0.5,
g = 0.6,
p = 0.7
)
ggplot(data = moose_two_stage_rates) +
geom_line(aes(x = years, y = adult), color = "red") +
geom_line(aes(x = years, y = juvenile), color = "blue") +
labs(
x = "Years",
y = "Moose"
)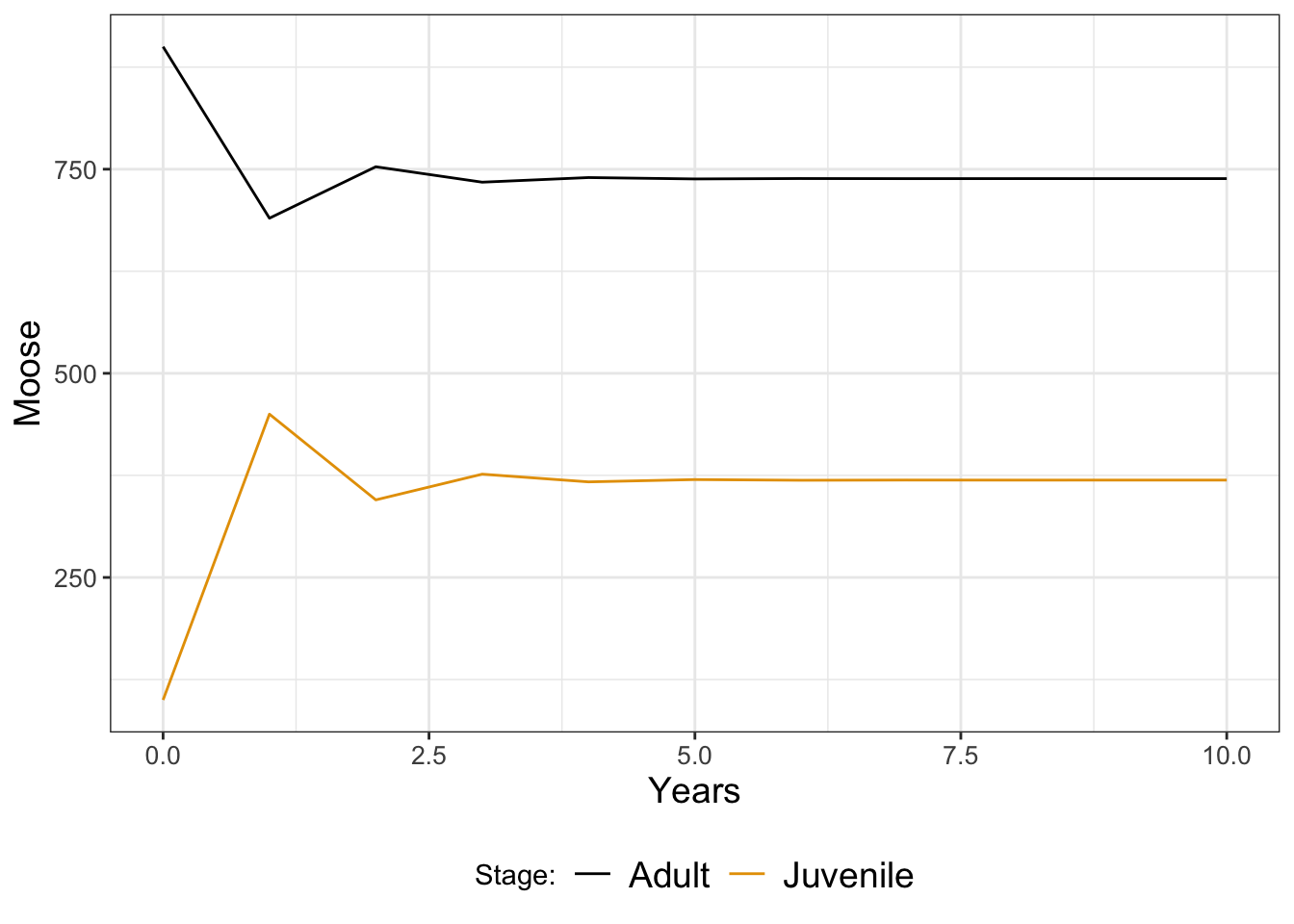
FIGURE 21.3: Simulation of a two stage moose population model.
Looking at Figure 21.3, it seems like both populations stabilize after a few years. We could further analyze this model for stable population states (in fact, it would be similar to determining eigenvalues as in Chapter 18). Additional extensions could also incorporate adjustments to the parameters \(f\), \(g\), and \(p\) in snow years (Exercise 21.5).
As you can see, introducing stochastic or random effects to a model yields some interesting (and perhaps more realistic) results. Next we will examine how computing can further explore stochastic models and how to generate expected patterns from all this randomness. Onward!
21.5 Exercises
Exercise 21.1 Re-run the moose population model with probabilities of adjusting to the deep snowpack at \(p = 0, \; 0.1, \; 0.9, \mbox{ and} \;1\). How does adjusting the probability affect the moose population after 10 years?
Exercise 21.2 Modify the function moose_snow so that runif(1) < snowfall_prob) is changed to runif(1) > snowfall_prob). How does that code change the resulting solution trajectories in Figure 21.2? Why is this not the correct way to code changes in the net birth rate in deep snowpacks?
Exercise 21.3 Modify the two stage moose population model (Equation (21.3)) with the following parameters and plot the resulting adult and juvenile populations:
- \(f = 0.6\), \(g = 0.6\), \(p = 0.7\)
- \(f = 0.5\), \(g = 0.6\), \(p = 0.4\)
- \(f = 0.3\), \(g = 0.6\), \(p = 0.5\)
You may assume \(M_{0} = 900\) and \(J_{0}=100\).
Exercise 21.4 You are playing a casino game. If you win the game you earn $10. If you lose the game you lose your bet of $10. The probability of winning or losing is 50-50 (0.50). You decide to play the game 20 times and then cash out your net earnings.
- Write code that is able to simulate this stochastic process. Plot your results.
- Run this code five different times. What do you think your long term net earnings would be?
- Now assume that you have a 40% chance of winning. Re-run your code to see how that affects your net earnings.
Exercise 21.5 Modify the two stage moose population model (Equation 21.5) to account for years with large snowdepths. In normal years, \(f=0.5\), \(g=0.6\), \(p=0.7\). However for snowy years, \(f=0.3\), \(g=0.6\), \(p=0.5\). Generate code that can account for these variable rates (similar to the moose population model). You may assume \(M_{0} = 900\), \(J_{0}=100\), and \(N\) (the number of years) is 30. Plot simulations when the probability of snowy winters is \(s=0.05\) \(s=0.10\), or \(s=0.20\). Comment on the long-term dynamics of the moose for these simulations.
Exercise 21.6 A population grows according the the growth law \(x_{t+1}=r_{t}x_{t}\).
- Determine the general solution to this discrete dynamical system.
- Plot a sample growth curve with \(r_{t}=0.86\) and \(r_{t}=1.16\), with \(x_{0}=100\). Show your solution for \(t=50\) generations.
- Now consider a model where \(r_{t}=0.86\) with probability 1/2 and \(r_{t}=1.16\) with probability 1/2. Write a function that will predict the population after \(t=50\). Show three or four different realizations of this stochastic process.
::: {.exercise #unnamed-chunk-259} (Inspired by Logan and Wolesensky (2009)) A rectangular preserve has area \(a\). At one end of the boundary of the preserve (contained within the area), is a small band of land of area (\(a_{b}\)) from which animals disperse into the wilderness. Only animals at that eged disperse. Let \(u_{t}\) be the number of animals in \(a\) at any time \(t\). The growth rate of all the animals in \(a\) is \(r\). The rate at which animals disperse from the strip is proportional to the fraction of the animals in the edge band, with proportionality constant \(\epsilon\).
- Draw a picture of the situation described above.
- Explain why the equation that describes the dynamics is \(\displaystyle u_{t+1}=r \, u_{t} - \epsilon \frac{a_{b}}{a} u_{t}\).
- Determine conditions on the parameter \(r\) as a function of the other parameters under which the population is growing.
:::