26.2 A stochastic system of equations

Let’s examine a stochastic system of differential equations. Here we will return to the lynx-hare model:

\[\begin{equation} \begin{split} \frac{dH}{dt} &= r H - b HL \\ \frac{dL}{dt} &=ebHL -dL \end{split} \end{equation}\]

In this case we still split each equation into the birth (\(\alpha\)) and death (\(\delta\)) parts: \[\begin{align*} \alpha & = \begin{cases} \frac{dH}{dt}: & r H \\ \frac{dL}{dt}: & ebHL\\ \end{cases} \\ \delta & = \begin{cases} \frac{dH}{dt}: & bHL \\ \frac{dL}{dt}: & dL\\ \end{cases} \end{align*}\]

To simulate this stochastic process, the setup of the code is similar to previous ways we solved systems of differential equations. Since we have a system of equations to compute the expected value and variance requires additional knowledge of matrix algebra, but that is already included in the function birth_death_stochastic

# Identify the birth and death parts of the DE:
birth_rate_pred <- c(dH ~ r*H, dL ~ e*b*H*L)
death_rate_pred <-  c(dH ~ b*H*L, dL ~ d*L)

# Identify the initial condition and any parameters
init_pred <- c(H=1, L=3)  # Be sure you have enough conditions as you do variables

# Identify the parameters
parameters_pred <- c(r = 2, b = 0.5, e = 0.1, d = 1)

# Identify how long we run the simulation
deltaT_pred <- .05    # timestep length
time_steps_pred <- 200   # must be a number greater than 1

# Identify the standard deviation of the stochastic noise
sigma_pred <- .1


# Do one simulation of this differential equation
out_pred <- birth_death_stochastic(birth_rate = birth_rate_pred,
                                       death_rate = death_rate_pred,
                                       init_cond = init_pred,
                                       parameters = parameters_pred,
                                       deltaT = deltaT_pred,
                                       n_steps = time_steps_pred,
                                       sigma = sigma_pred)

# Visualize the solution
ggplot(data = out_pred) +
  geom_line(aes(x=t,y=H),color='red') +
  geom_line(aes(x=t,y=L),color='blue') +
labs(x='Time',
     y='Lynx (red) or Hares (blue)')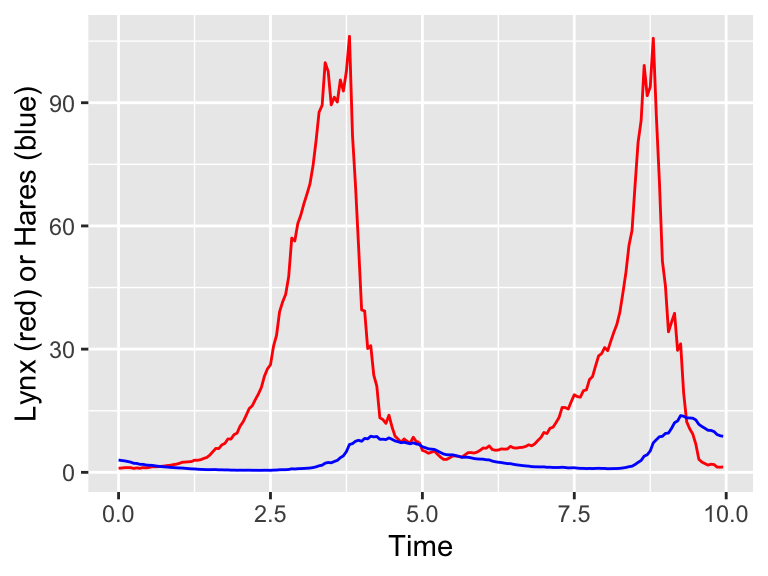
One realization of the stochastic predator-prey model.

Figure 26.4: One realization of the stochastic predator-prey model.

Excellent! Notice how Figure 26.4 has stochasticity in the variables for both H and L. The next step would be to do many simulations and then compute the ensemble average. First let’s compute the individual simulations:

# Many solutions
n_sims <- 100  # The number of simulations

# Compute solutions
pred_sim <- rerun(n_sims) %>%
  set_names(paste0("sim", 1:n_sims)) %>%
  map(~ birth_death_stochastic(birth_rate = birth_rate_pred,
                                       death_rate = death_rate_pred,
                                       init_cond = init_pred,
                                       parameters = parameters_pred,
                                       deltaT = deltaT_pred,
                                       n_steps = time_steps_pred,
                                       sigma = sigma_pred)
) %>%
  map_dfr(~ .x, .id = "simulation")

The above code may take a while to complete - but this is certainly shorter than computing these all by hand! In order to make the spaghetti plot, we will plot the variables \(H\) and \(L\) separately.

# Plot the hares first:
ggplot(data = pred_sim) +
  geom_line(aes(x=t,y=H,color=simulation)) +
  ggtitle("Spaghetti plot for hares in the predator-prey SDE") +
  guides(color="none")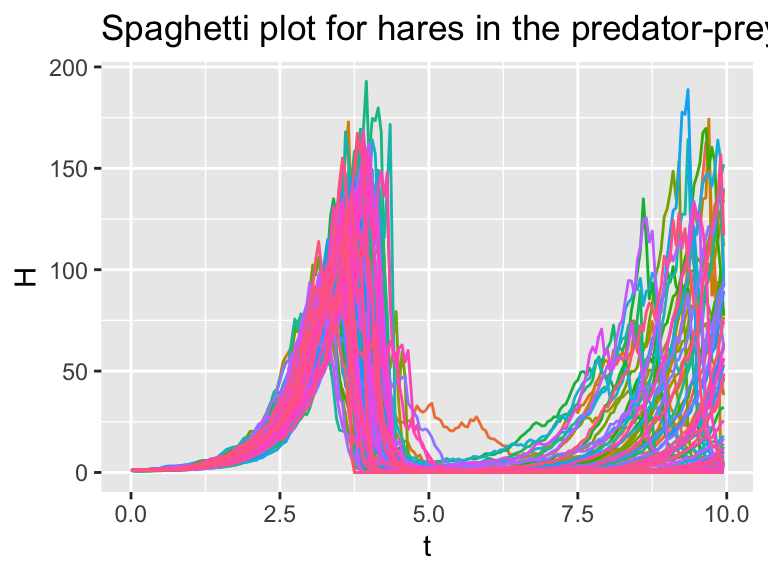
Several different realizations of the stochastic predator-prey system.

Figure 26.5: Several different realizations of the stochastic predator-prey system. 

# Then plot the lynx:
ggplot(data = pred_sim) +
  geom_line(aes(x=t,y=L,color=simulation)) +
  ggtitle("Spaghetti plot for lynx in the predator-prey SDE") +
  guides(color="none")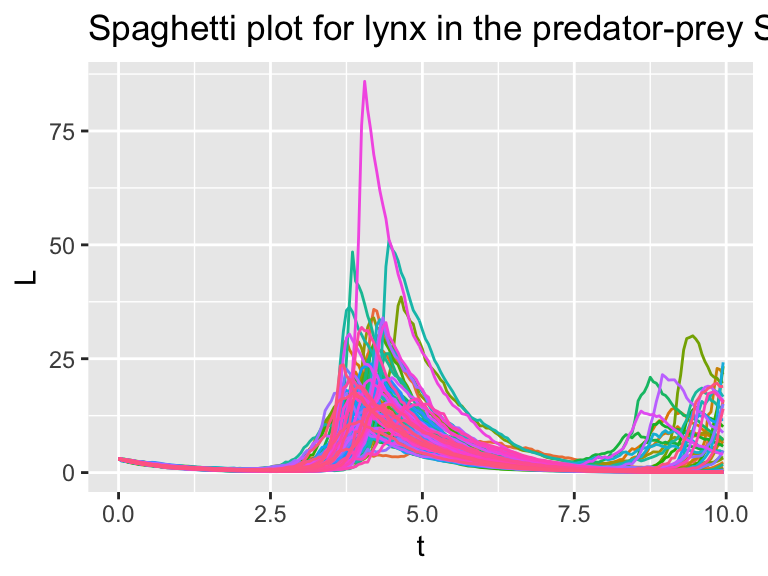
Several different realizations of the stochastic predator-prey system.

Figure 26.6: Several different realizations of the stochastic predator-prey system.

For the ensemble average plots, we will first utilize the pivot_longer command, group and then summarize:

 ### Summarize the variables
summarized_pred_sim <- pred_sim %>%
  pivot_longer(cols=c("H","L")) %>%
  group_by(name,t) %>%  # All simulations will be grouped at the same timepoint.
  summarise(value = quantile(value, c(0.25, 0.5, 0.75)), q = c("q0.025", "q0.5", "q0.975")) %>%
  pivot_wider(names_from = q, values_from = value)
## `summarise()` has grouped output by 'name', 't'. You can override using the `.groups` argument.
# Let's take a look at the resulting data frame
glimpse(summarized_pred_sim)
## Rows: 400
## Columns: 5
## Groups: name, t [400]
## $ name   <chr> "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"…
## $ t      <dbl> 0.00, 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.5…
## $ q0.025 <dbl> 1.0000000, 0.9739683, 0.9704827, 0.9850577, 0.9916619, 1.031269…
## $ q0.5   <dbl> 1.000000, 1.024874, 1.046321, 1.050366, 1.075298, 1.140154, 1.1…
## $ q0.975 <dbl> 1.000000, 1.080082, 1.091934, 1.139265, 1.212339, 1.248552, 1.3…

Let’s break this down:

  • The data frame pred_sim has columns simulation, t, H, and L. We want to group each variable by the time t. In order to do that efficiently we need to pivot the data frame longer. By applying the command pivot_longer(cols=c("H","L")) we will still have 4 columns, but this time they are called simulation, t, name, and value. The column name is a categorical variable that is either H or L (the columns we made longer), and the column value has the numerical values for both at each time.
  • We then group by the column name first, and then by time.
  • The remainder of the code is similar to how we computed the ensemble average above.

The tricky part is that resulting columns of summarized_pred_sim are name, t, and the quantile values. This may seem a challenge to plot, but we can easily make a small multiples plot with the command facet_grid:

ggplot(data = summarized_pred_sim) +
  geom_line(aes(x = t, y = q0.5)) +
  geom_ribbon(aes(x=t,ymin=q0.025,ymax=q0.975),alpha=0.2) +
  facet_grid(. ~ name)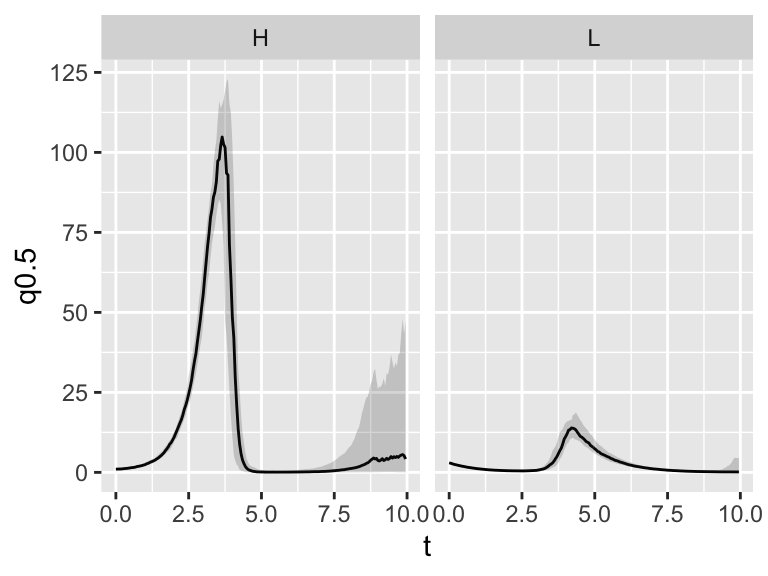
Ensemble average plot of the predator-prey system.

Figure 26.7: Ensemble average plot of the predator-prey system.

The last command facet_grid(. ~ name) splits the plot up into different panels (or facets) by the column name. So easy to make!

If you are feeling a little overwhelmed by all these new plotting commands - don’t worry. You can easily modify these examples for a different systme of differential equations. You’ve got this!