3.4 Other types of functional responses

In several examples we have seen a rate of change proportional to the current population, as in the rate of growth of the hare population is \(rH\). This is one example of what we would call a functional response. Another type of functional response assumes that the rate reaches a limiting value proportional to the population size, so \(\displaystyle \frac{dH}{dt} = \frac{rH}{1+arH}\). This is an example of a type II functional response. Finally, the type II response has also been generalized (a type III functional response) \(\displaystyle \frac{dH}{dt} = \frac{rH^{2}}{1+arH^{2}}\). Figure 3.6 shows all three functional responses together:

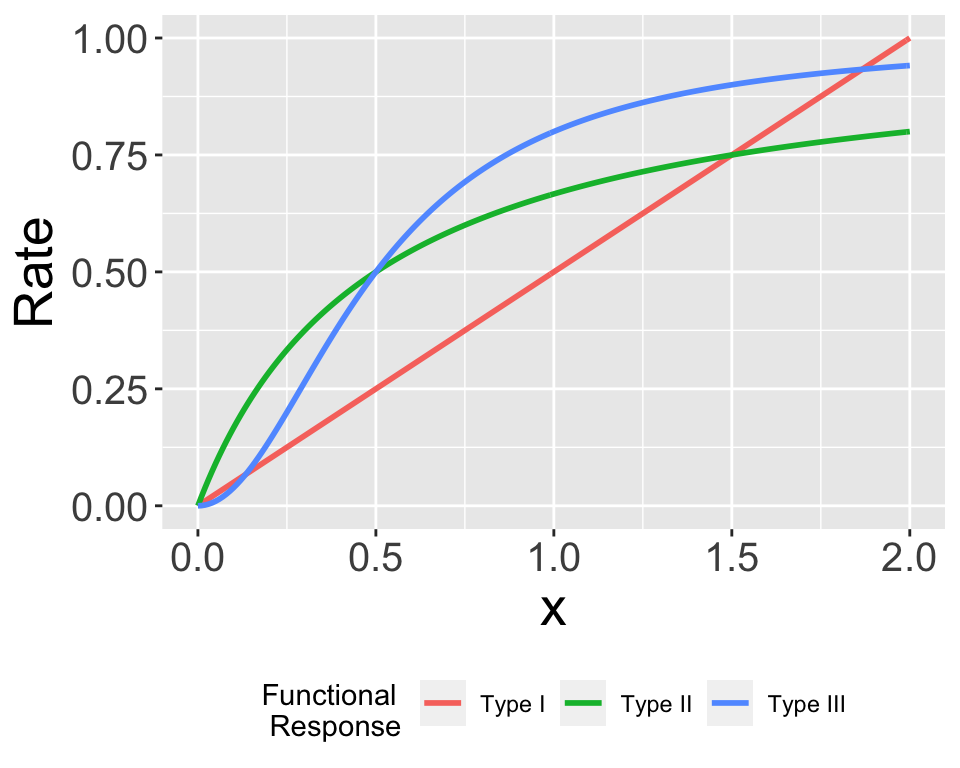
Figure 3.6: Comparison between Type I - Type III functional responses.

Notice the limiting behavior in the Type II and Type III functional responses. These responses are commonly used in ecology and predator-prey dynamics and in problems of how animals search for food.