16.1 Determining equilibrium solutions

To determine an equilbrium solutions for a system of differential equations we first need to find the intersection of different nullclines. We do this by setting each of the rate equations ($\displaystyle \frac{dx}{dt}$ or $\displaystyle \frac{dy}{dt}$) equal to zero. Equation (16.1) has two nullclines:

\[\begin{equation} \begin{split} \frac{dx}{dt} = 0 &\rightarrow y-1 = 0\\ \frac{dy}{dt} = 0 & \rightarrow x^{2}-1 = 0 \end{split} \tag{16.2} \end{equation}\]

So solving for both nullclines in Equation (16.2) we have that $y=1$ or $x = \pm 1$. You can visually see the phaseplane with the nullclines in Figure 16.4.

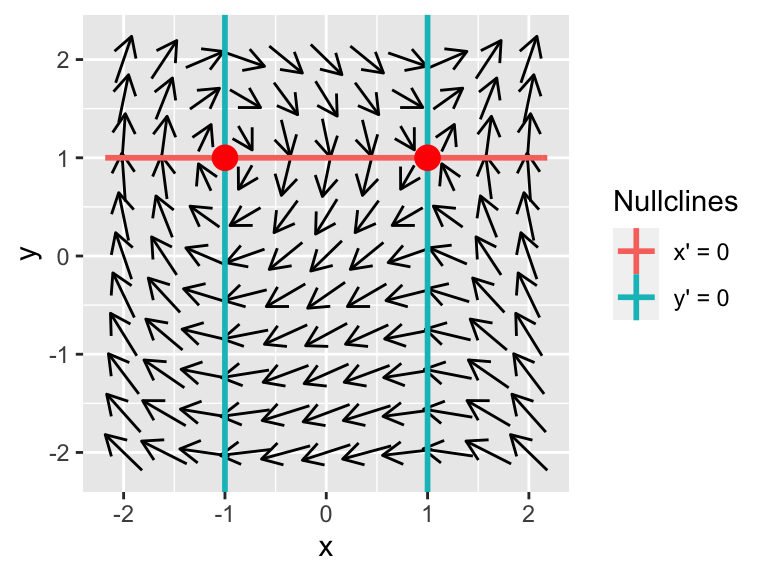
$Phaseplane for $x'=y-1$ and $y'=x^{2}-1$.$

Figure 16.4: Phaseplane for $x'=y-1$ and $y'=x^{2}-1$.

Remember: equilibrium solutions occur when two different nullclines intersect.

Let’s try another example:

\[\begin{equation} \begin{split} \frac{dx}{dt} &= x-0.5yx \\ \frac{dy}{dt} &= yx -y^{2} \end{split} \tag{16.3} \end{equation}\]

Figure 16.5 shows the phaseplane for this example. Can you guess where an equilibrium solution would be?

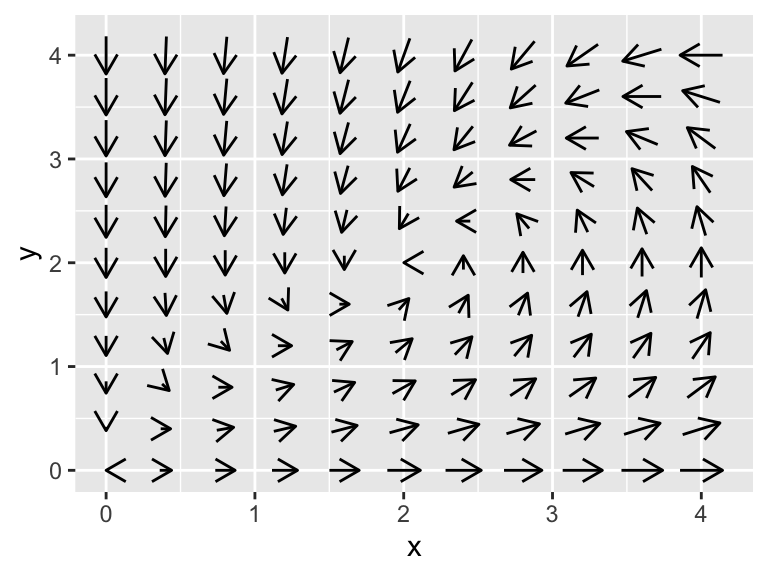
$Phaseplane for $x'=x-0.5xy$ and $y'=yx=y^{2}$.$

Figure 16.5: Phaseplane for $x'=x-0.5xy$ and $y'=yx=y^{2}$.

Let’s find the equations for the nullclines:

\[\begin{equation} \begin{split} \frac{dx}{dt} = 0 & \rightarrow x-0.5yx = 0 \\ \frac{dy}{dt} = 0 & \rightarrow yx -y^{2} = 0 \end{split} \end{equation}\]

The algebra is becoming a little more involved. Factoring $x-0.5yx = 0$ we have $x \cdot (1 - 0.5 y) = 0$, so either $x=0$ or $y=2$. Factoring the second equation we have $y \cdot (x - y) = 0$, so either $y=0$ or $x=y$. Notice how this second nullcline is a function of $x$ and $y$.

For Equation (16.3) the equilibrium solutions are $(0,0)$, $(2,2)$. You may be tempted to think that $(0,2)$ is also an equilibrium solution - however - $x=0$ and $y=2$ are equations for the $x$ nullcline. It is easy to forget, but equilibrium solutions are determined from the intersection of distinct nullclines.